Time-Resolved Particle Image Velocimetry (TR-PIV) applies the principles and techniques of PIV at a high sampling rate. More specifically, to be considered time-resolved the sampling rate must be twice the frequency of a given phenomena of interest. This ability to sample high frequency flow fluctuations allows for insight into turbulence effects both directly and via additional post processing. Fig. 1 shows an animation of TR-PIV vector maps. Notice how the flow is continuous in nature, and is thus temporally resolved.

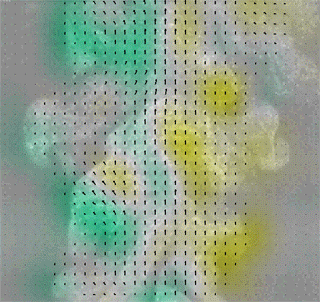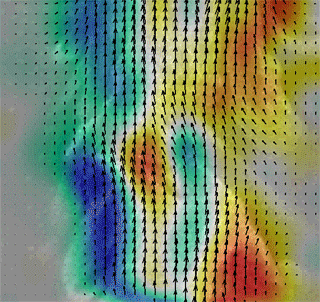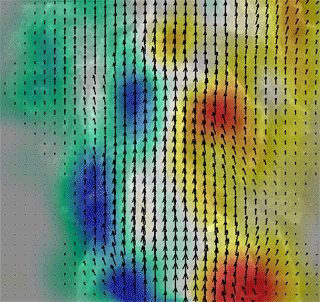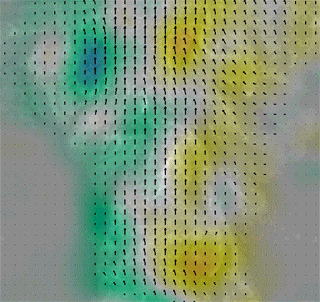
Fig 1. TR-PIV of a turbulent jet.

The direct measurement of the level of fluctuation in a turbulent flow often takes the form of a root-mean-square (RMS) value. Here, if a single mean velocity component at a single point in the measured domain, U, can be calculated as:

\( U = \frac{\sum{}{}u_i}{N} \)

where u_i is the instantaneous amplitude of this velocity component and N is the total number of TR-PIV vectors included in the measurement, then the RMS of fluctuations of that single velocity component can be calculated as:

\( u_{RMS} = \sqrt{\frac{\sum{}{}u_i – U}{N}} \)

As the sampling rate and spatial resolution requirements of TR-PIV are directly dictated by the phenomena being measured, these being mutually exclusive quantities in most cameras, convergence checks must be employed to ensure that both the mean and turbulent statistics of the measured flow have converged within an allotted number of samples. An example of this kind of convergence check can be seen in Fig. 2.

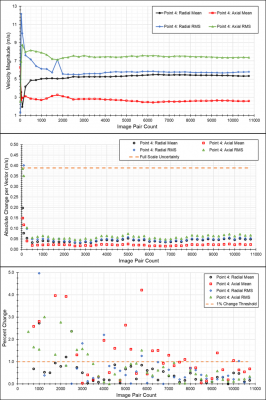
Fig. 2. Convergence check of a point within a turbulent swirling flow.

Here, the first check is to ensure that the mean and turbulent statistics become visually asymptotic. The second check is to ensure that the change in the mean and turbulent statistics is less than the full-scale PIV uncertainty. The final check is to ensure that the change in statistics per vector ‘bin’ (100 vectors, 1000 vectors, etc.) is less than 1%.

Fig. 3. Time Resolved PIV Experimental Setup